Introduction To Performance

The Concepts of Parallel Performance

Parallel computing used to be a very specialized domain; but now even making the best use of your laptop, which almost certainly has multiple independant computing cores, requires understanding the basic concepts of performance in a parallel environment.

Most fundamentally, parallel programming allows three possible ways of getting more and better science done:

Running many copies of the same program If you have a program that works in serial, having many processors available to you allows you to run many copies of the same program at once, improving your througput. This (can be) a sort of trivial use of parallel computing and doesn't require very specialized hardware, but it can be extremely useful for, for instance, running parameter studies or sensitivity studies. Best of all, this is essentially guaranteed to run efficiently if your serial code runs efficiently! Because this doesn't require fancy hardware, it is a waste of resources to use the Tightly Coupled System for these sorts of tasks and instead they must be run on the General Purpose Cluster.
Running the same program on many processors. This is what most people think of as parallel computing. It can take a lot of work to make an existing code run efficiently on many processors, or to design a new code to make use of these resources, but when it works, one can achieve a substantial speedup of individual jobs. This might mean the difference between a computation running in a feasible length of time for a research project or taking years to complete --- so while it may be a lot of work, it may be your only option. To determine whether your code runs well on many processors, you need to measure speedup and efficiency; to see how many processors one should use for a given problem you must run strong scaling tests.
Running larger problems. One achieves speedup by using more processors on the same problem. But by running your job in parallel you may have access to more resources other than just processors --- for instance, more memory, or more disks. In this case, you may be able to run problems that simply wouldn't be possible on a single processor or a single computer; one can achieve significant sizeup. To find how large a problem one can efficiently run, one measures efficiency and runs weak scaling tests.

Of course, these aren't exclusive; one can take advantage of any combination of the above. It may be that your problem runs efficiently on 8 cores but no more; however, you may be able to get use of more processors by running many jobs to explore parameter space, and already on 8 cores you may be able to consider larger problems than you can with just one!

Throughput

Throughput is the most fundamental measure of performance, and the one that ultimately most matters to most computational scientists -- if you have N computations that you need to have done for your research project, how quickly can you get them done? Everything else we'll consider here is just a way of increasing throughput T: $LaTeX: T = \frac{\mathrm{Number}\,\mathrm{of}\,\mathrm{computations}}{\mathrm{Unit}\,\mathrm{time}} .$

If you have many indepdendent computations to perform (such as a parameter study or a sensitivity study) you can increase throughput almost arbitrarily by running them alongside each other at the same time, limited only by the number of processors available (or the wait time in the queue, or the disk space available, or some other external resource constraint). This approach obviously doesn't work if you only have one computation to perform, or if later computations require the output from previous ones. In these cases, or when the individual jobs take infeasibly long, or cannot be performed on only one processor, one must resort to also using parallel programming techniques to parallelize the individual jobs.

Compute Time

Fundamental to everything else that follows is measuring the amount of time a computation takes on some problem size/amount of work $LaTeX: N$ and some number of processors $LaTeX: P$ . We'll done this by $LaTeX: t(N,P)$ . The easiest way to measure this time is with the time command that comes on most flavours of Unix in /bin/time or /usr/bin/time:

/bin/time myprogram
...normal program output...
658.44user 0.85system 10:59.41elapsed

The format of the times output at the end may vary from system to system, but the basic information returned will be the same. The real or elapsed time listed is the actual Wallclock time that elapsed during the run, user or cpu is the CPU time that was actually spent doing your computation, and the system time is the system time that was spent doing system-related things during the run, such as waiting for file input/output. Our goal will be to reduce the real wallclock time that the simulation takes as much as possible while still making efficient use of the resources available.

Parallel Speedup

The speedup of an individual job with some amount of work $LaTeX: N$ as you go from some running it serially to running on $LaTeX: P$ is simply:

$LaTeX: S(N,P) = \frac{t(N,P=1)}{t(N,P)} .$

That is, the time it takes to run the computation on P vs on one processor. The way this is usually done is to run the parallel code on $LaTeX: P$ and on $LaTeX: 1$ processor and take the ratio of the two times; but this is a form of cheating, as the parallel version of the code will generally have overheads (even in the one-processor case) compared to the best available serial-only version of the code. The best thing to do in considering the efficiency of the parallelization to compare the parallel code to the best available serial code that does the same job.

If you are considering the speedup of a problem that doesn't fit onto one processor, of course, the concept of speedup can be generalized; one needn't start at $LaTeX: P=1$ .

It should go without saying that, while developing your parallel code and during performance tuning, you get the same results with multiple processors as with some `known good' serial test case; it is even easier to introduce bugs in parallel code than it is in serial code!

Efficiency

Once you have a parallel code and some timing results one can look at how efficiently you are making use of the resources as you use more and more processors. The parallel efficiency of a computation of some fixed work size running on $LaTeX: P$ processors as compared to the $LaTeX: P=1$ case is

$LaTeX: E = \frac{S(N,P)}{P}$

That is, if you get a speedup of $LaTeX: 8 \times$ in going from one to eight processors, you are at 1.00 or 100% efficiency; anything less and you are at lower efficiency. It isn't uncommon to achieve greater than 100% parallel efficiencies for small numbers of processors for some types of problems; as you go to more processors, you also have more processor cache, and thus more of the problems data can fit into fast cache. This is called super-linear speedup and sadly seldom extends out to very many processors.

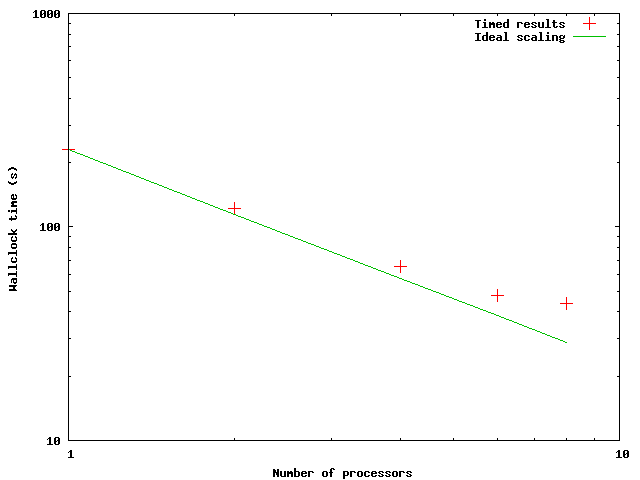
Strong Scaling Tests

$LaTeX: P$	$LaTeX: t(N,P)$	$LaTeX: S(N,P)$
3:50.1 \| \|	-	2:02.6 \| 1.87x \| 94 %
1:05.2 \| 3.52x \| 88 %
47.8 \| 4.81 \| 80 %
43.6 \| 5.28 \| 66%

An example of a strong scaling test

Weak Scaling Tests

Performance Tuning

Serial Performance

Worrying about parallel performance before the code performs well with a single task doesn't make much sense! Profiling your code when running with one task allows you to spot serial `hot spots' for optimization, as well as giving you more detailed understanding of where your program spends its t

/bin/time

gprof

vtune, openspeedshop (GPC)

Xprofiler, peekperf, hpmcount (p6)

Parallel Performance Tools

scalasca (TCS,GPC)

intel thread tuner

openspeedshop (MPI: GPC)

Common OpenMP Performance Problems

Common MPI Performance Problems

Overuse of MPI_BARRIER

Many Small Messages

Typically, a the time it takes for a message of size n to get from one node to another can be expressed in terms of a latency l and a bandwidth b, $LaTeX: t_c = l + \frac{n}{b} .$ For small messages, the latency can dominate the cost of sending (and processing!) the message. By bundling many small messages into one, you can amortize that cost over many messages, reducing the time spent communicating.

$LaTeX: P$	$LaTeX: t(N,P)$	$LaTeX: S(N,P)$
3:50.1 \| \|	-	2:02.6 \| 1.87x \| 94 %
1:05.2 \| 3.52x \| 88 %
47.8 \| 4.81 \| 80 %
43.6 \| 5.28 \| 66%