Modern Fortran for FORTRAN77 users

Jonathan Dursi

This is the Wiki-fied version of the slides used for the Modern Fortran course at SciNet. To follow along, with both the examples and the hands on, you will want to download the source code and make sure you have a working Fortran 2003 compiler.

Course Overview

Intro, History (10 min)
New syntax (30 min)
Hands On 1(60 min)
Functions, Modules (45 min)
#Hands On 2 (30 min)
Lunch (1 hr)
New Array Features (15 min)
Hands on #3 (30 min)
Pointers & Interfaces (30 min)
Hands on #4 (30 min)
Derived Data Types and Objects (30 min)
Interoperability with C,Python (30 min)
Coarrays (30 min)

A Brief History of Fortran

Only major compiled programming language designed speciﬁcally for scientiﬁc programming.
Powerful array operations; many mathematical functions (Bessel functions!) built in; designed to enable compiler optimizations for fast code
Oldest (54-57 yrs) still-used programming language.
Most people come to Fortran via being given old code by someone.
Can’t understand the old code, or quirks of modern language, without understanding it’s history
1957 - J.W. Backus et al. In Proceedings Western Joint Computer Conference, Los Angeles, California, February 1957.
IBM 704
(Arguably) ﬁrst modern compiled programming language.
Idea of compilers at all was controversial at time.

(from http://www.softwarepreservation.org/projects/FORTRAN/ )

(from http://en.wikipedia.org/wiki/File:Fortran_acs_cover.jpeg )

FORTRAN (1957)

Fixed-column format to simplify punched cards
C in column 1 - comment
Line labels in cols 2-5
Continuation character in col 6
Code in cols 7-72.
Continued until Fortran90!
Variables did not need declaration
Any variables used starting with i,j,k,l,m,n were assumed integer, all others real.
Saved punched cards.
Idea is with us today terrible idea.
Already had multidimensional arrays!

(from http://en.wikipedia.org/wiki/File:FortranCardPROJ039.agr.jpg )

Incremental changes

FORTRAN II (1958) - subroutines and functions (good!) common blocks (terrible, terrible).
Still machine dependent (READ INPUT TAPE)
FORTRAN III - inline assembly - never released
FORTRAN IV (1961) - removed machine dependancies

FORTRAN66

With implementation of standard, loss of machine dependency, started gaining wide use on many computers
Many implementations
double precision, complex, logical types
intrinsic and external routines

FORTRAN77

The most common to see “in the wild” of old code today
if/else/endif, better do loops, control of implicit typing
Character strings, saved variables, IO improvements
Approved in 1978, beginning long tradition of “optimistic” naming of standards by year.

The interregnum

Programming languages and techniques were moving quite quickly
Several attempts were made to make new version, but standardization process very slow, failed repeatedly.
Absent new real standard, implementations began to grow in many different directions
Some extensions became quasi-standard, many were peculiar to individual compilers.

Fortran90

Enormous changes; the basis of modern Fortran (not FORTRAN!)
Free form, array slices, modules, dynamic memory allocation, derived types...
Changes so major that took several years for compilers to catch up.
Modern fortran

And since...

Fortran95 - modest changes to Fortran90, killed off some deprecated F77 constructs.
Fortran 2003 - bigger change; object-oriented, C interoperability. Most compilers have pretty good F2003 support.
Fortran 2008 - mostly minor changes, with one big addition (coarray), other parallel stuff. Compiler-writers getting there.

F90, F95, F2003, F2008..

We won’t distinguish between versions; we’ll just show you a lot of useful features of modern fortran.
Will only show widely-implemented features from 2003 and 8, with exception of coarrays; these are being implemented and are very important.

New Format, New Syntax

Free Format: some highlights

Columns no longer signiﬁcant; can start at left margin
Implicit none. Always, always use.
Variable declaration syntax changed (more later)
Lines can be up to 132 char long; to continue, put & at end of line.
! for comments; comments out rest of line.
Numeric line labels are strongly discouraged, but control structures can be named (more later)
<, > vs .lt., .gt.
<=, >= vs .le., .ge.
==, /= vs .eq., .neq.
Program, procedure can contain other procedures
“program x” or “function y” ended by “end program x” or “end function y”
Case doesn’t matter (except strings)
Lines can start anywhere, can be 132 cols long
Continue with an & at end of line
Can continue a single line 255 times
Comments - !, can start anywhere, comments out rest of line
Compilers can usually handle both old ﬁxed format and modern free format, but not within the same ﬁle.
(From samples/freeform/freeform.f90)

<source lang="fortran"> program example

   implicit none
   integer, parameter :: npts = 10000
   real, parameter :: startx=0., endx=1.
   real, parameter :: dx = (endx-startx)/npts

   real :: integral, xleft, xright, xmid
   integer :: i

   if (npts < 2) then
       print *,'Too few points!'
   else
       integral = 0.  ! Simpson's Rule
       xleft = 0.

  int: do i=0,npts-1
           xright = (i+1)*dx
           xmid = (xleft+xright)/2.

           integral = integral + (dx/6.)*(f(xleft) + 4.*f(xmid) + &
                                          f(xright))
           xleft = xright
        end do int

        print *,'Numerical integral is ', integral
        print *,'Exact soln is ', (endx-startx)/2.  - &
                                    (sin(2*endx)-sin(2*startx))/4.
    endif

contains

   function f(x)
       implicit none
       real :: f
       real, intent(in) :: x
       f = sin(x)**2
   end function f

end program example </source>

Variable Declarations

Implicit none turns off all implicit typing.
Was a common F77 extension, but not part of a standard.
DO THIS. Without, (eg) variable typos don’t get caught.
This is going to be a recurring theme for several features.
You do a little more typing and make things explicit to compiler.
Then compiler can catch errors, optimize, better.
The “::” separating type and name is new
Type declarations can now have a lot more information
Many attributes of variables set on declaration line
:: makes it easier for you, compiler, to see where attributes stop and variable names begin
Parameter attribute for values which will be constants.
Compiler error if try to change them.
Useful for things which shouldn’t change.
F77 equivalent:

<source lang="fortran"> integer i parameter (i=5) </source>

Initialization of variables at declaration time
- Required for parameters (because can’t change them later), can be done for other variables.
- Can do anything that compiler can ﬁgure out at compile time, including math with other parameters.

   implicit none
   integer, parameter :: npts = 10000
   real, parameter :: startx=0., endx=1.
   real, parameter :: dx = (endx-startx)/npts

   real :: integral, xleft, xright, xmid
   integer :: i

</source>

Variable Initialization

Initializing variables this way gives unexpected behaviour in functions/subroutines “for historical reasons”.
Initialized variables given the “save” attribute
eg, integer, save, i=5
Value saved between calls. Can be handy - but not threadsafe.
Initialization done only ﬁrst time through.
Not a problem for main program, parameters.

...

subroutine testvarinit

   implicit none
   integer :: i = 5

   print '(A,I3)', 'On entry; i = ', i
   i = 7
   print '(A,I3)', 'Now set;  i = ', i

end subroutine testvarinit

...

program initialization

   use inittest

...

   call testvarinit
   call testvarinit

...

end program initialization

</source>

( From samples/variables/initialization/initialization.f90)

<source lang="bash"> $ gfortran initialization.f90 -o initialization $ ./initialization On entry; i = 5 Now set; i = 7 On entry; i = 7 Now set; i = 7 </source>

Real Kinds

Reals, Double precisions, really different “kinds” of same “type” - ﬂoating point real numbers.
Kinds introduced to give enhanced version of functionality of non-standard but ubiquitous constructs like REAL*8
real32, real64 deﬁned in iso_fortran_env in newest compilers (gfortran 4.6, ifort 12)
selected_real_kind(N): returns kind parameter for reals with N decimal digits of precision
Default real is generally 4-byte (32bit) real, has 6 digits of precision and a range of 37 in the exponent.
Many built-in (‘intrinsic’) functions which give info about properties of a variable’s numerical type.
precision - #digits of precision in decimal * range - of exponent
tiny, huge - smallest, largest positive represented number
epsilon - machine epsilon
several others

<source lang="fortran"> program realkinds

   use iso_fortran_env
   implicit none

   real :: x
   real(kind=real32) :: x32
   real(kind=real64) :: x64
   real(kind=real128):: x128

   real(kind=selected_real_kind(6)) :: y6
   real(kind=selected_real_kind(15)):: y15

   print *,'Default:'
   print *, precision(x), range(x)
   print *,'Real32:'
   print *, precision(x32), range(x32)
   print *,'Real64:'
   print *, precision(x64), range(x64)
   print *,'Real128:'
   print *, precision(x128), range(x128)

   print *,

   print *,'Selected Real Kind 6:'
   print *, precision(y6), range(y6)

   print *,'Selected Real Kind 15:'
   print *, precision(y15), range(y15)

end program realkinds </source> (from samples/variables/kinds/realkinds.f90)

<source lang="bash"> $ ./realkinds

Default:
          6          37
Real32:
          6          37
Real64:
         15         307
Real128:
         18        4931

Selected Real Kind 6:
          6          37
Selected Real Kind 15:
         15         307

</source>

Integer Kinds

Similar constructs for integers
selected int kind(N): kind can represent all N-digit decimal numbers.
huge(N): largest positive number of that type samples/variables/kinds/intkinds.f90

<source lang="fortran"> program integerkinds

   use iso_fortran_env
   implicit none
   
   integer :: i
   integer(kind=int8)  :: i8
   integer(kind=int16) :: i16
   integer(kind=int32) :: i32
   integer(kind=int64) :: i64

   integer(kind=selected_int_kind(6)) :: j6
   integer(kind=selected_int_kind(15)):: j15

   print *,'Default:'
   print *, huge(i)
   print *,'Int8:'
   print *, huge(i8)
   print *,'Int16:'
   print *, huge(i16)
   print *,'Int32:'
   print *, huge(i32)
   print *,'Int64:'
   print *, huge(i64)
   
   print *,

   print *,'Selected Integer Kind 6:'
   print *, huge(j6)
   
   print *,'Selected Integer Kind 15:'
   print *, huge(j15)

end program integerkinds </source>

(from samples/variables/kinds/intkinds.f90)

<source lang="bash"> $ ./intkinds

Default:
 2147483647
Int8:
 127
Int16:
 32767
Int32:
 2147483647
Int64:
 9223372036854775807

Selected Integer Kind 6:
 2147483647
Selected Integer Kind 15:
 9223372036854775807

</source>

Strings

Character types are usually used for strings
Specify length
Padded by blanks
Intrinsic trim() gets rid of blanks at end
Can compare strings with <,>,==, etc.
Concatenate with //
Characters have kinds too
gfortran has partial support for selected_char_kind(“ISO_10646”) for unicode strings.

<source lang="fortran"> program strings

   implicit none
   character(len=20) :: hello 
   character(len=20) :: world
   character(len=30) :: helloworld

   hello = "Hello"
   world = "World!"
   
   helloworld = trim(hello) // " " // trim(world)
   
   print *, helloworld

   if (hello < world) then
       print *, '<', hello, '> is smaller.'
   else
       print *, '<', world, '> is larger.'
   endif

end program strings </source>

(from samples/variables/strings/strings.f90)

<source lang="bash"> $ ./strings

Hello World!                  
<Hello               > is smaller.

</source>

Array declarations

Array declarations have changed, too:
dimension is now an attribute
Can easily declare several arrays with same dimension

<source lang="fortran"> program arrays

   implicit none
   real, dimension(3) :: x, y

   x = [1,2,3]
   y = 2*x

   print *, x
   print *, y

end program arrays </source> ( from samples/variables/arrays/arrays.f90) <source lang="bash"> $ ./arrays

  1.0000000       2.0000000       3.0000000    
  2.0000000       4.0000000       6.0000000

</source>

Do loops

Do loops syntax has had some changes
do/enddo - was a common extension, now standard.
All constructs now have end constructname to end.
Named constructs (program, subroutine) require, eg, end program doi.
Helps catch various simple errors (mismatched ends, etc.)

<source lang="fortran"> program doi

       implicit none
       integer :: i

       do i=1,10
           print *, i, i**2, i**3
       enddo

end program doi </source> ( from samples/variables/doloops/doi.f90 ) <source lang="bash"> $ ./doi

          1           1           1
          2           4           8
          3           9          27
          4          16          64
          5          25         125
          6          36         216
          7          49         343
          8          64         512
          9          81         729
         10         100        1000

</source>

Named loops

Can name control structures like do, if statements now, too.
Handy for documentation, or to distinguish deeply-nested loops.
Again, can help catch mismatched loops.
enddo or end do; fortran isn’t picky about spaces.

<source lang="fortran"> program nameddo

   implicit none
   integer :: i, j

   outer: do i=1,3
       inner: do j=1,3
           print *, i, j, i*i+j*j
       enddo inner
   end do outer

end program nameddo </source> ( from samples/variables/doloops/nameddo.f90 ) <source lang="bash"> $ ./nameddo

          1           1           2
          1           2           5
          1           3          10
          2           1           5
          2           2           8
          2           3          13
          3           1          10
          3           2          13
          3           3          18

</source>

Cycle/exit

Do loops don’t even need a i=1,n
do/enddo
Will loop forever
Can control looping with cycle, exit
exit - exits loop. (exit loopname can exit out of nested loops)
cycle - jumps back to do

<source lang="fortran"> program cycleexit

   implicit none
   integer :: i

   do 
       print *, 'Enter a number between 1-13'
       read *,  i
       if (i>=1 .and. i<=13) exit
       print *, 'Wrong; try again.'
   enddo

   print *, 'Good; you entered ', i

end program cycleexit </source> ( from samples/variables/doloops/cycleexit.f90 ) <source lang="bash"> $ more cycleexit-out.txt $ ./cycleexit

Enter a number between 1-13

23

Wrong; try again.
Enter a number between 1-13

-1

Wrong; try again.
Enter a number between 1-13

12

Good; you entered           12

</source>

Do while

do while - repeats as long as precondition is true.
Seems like it should be useful, but in practice, just do/enddo with exit condition is usually cleaner.

<source lang="fortran"> program dowhile

   implicit none
   integer :: i

   i = -1  
   do while (i < 1 .or. i > 13)
       print *, 'Enter a number between 1-13'
       read *,  i
       if (i<1 .or. i>13) print *, 'Wrong; try again.'
   enddo

   print *, 'Good; you entered ', i

end program dowhile </source> ( from samples/variables/doloops/dowhile.f90 )

Hands On 1

In workedexample/f77 is a simpliﬁed, F77ized version of a ﬂuid-dynamics code from Ue-Li Pen, CITA, U of Toronto (http://www.cita.utoronto.ca/~pen/MHD/)
For the purposes of this class, we've turned it from a perfectly good f90 code to something that looks more like something your supervisor would dust off and give to you.
Today we’ll be translating this version into a very modern Fortran
Compile (using make) and run (./hydro)
Outputs a .pbm ﬁle; use “display dens.pbm” to see the result of dense blob of ﬂuid moving through a light medium.
In workedexamples/freeform, have partly converted the program to new freeform format, with enddos, ending procedures, implicit nones, and new variable declaration syntax.
Finish doing so - just need to do program hydro, subroutine color, subroutine outputpbm, function cﬂ. Fix indenting (Don't need to start at col 7 anymore).
~1 hr (for getting logged in and everything working)

Procedures and Modules

Several enhancements to how procedures (functions, subroutines) are deﬁned
Modules are ways of organizing procedures, deﬁnitions, into sensible units for ease of code maintenance, clarity

Modules

Easiest to show by example
Here, the gravity module deﬁnes a constant, and contains a function
Main program “use”s the module, has access to both.
“Use” goes before “implicit none”

<source lang="fortran"> module gravity

   implicit none
   real, parameter :: G  = 6.67e-11   ! MKS units

contains

   real function gravforce(x1,x2,m1,m2)
       implicit none
       real, dimension(3), intent(in) :: x1,x2
       real, intent(in) :: m1, m2
       real :: dist

       dist = sqrt(sum((x1-x2)**2))
       gravforce = G * m1 * m2 / dist**2
   end function gravforce

end module gravity

program simplemod

   use gravity
   implicit none

   print *, 'Gravitational constant = ', G
   print *, 'Force between 2 1kg masses at [1,0,0] &
             &and [0,0,1] is'

   print *, gravforce([1.,0.,0.],[0.,0.,1.],1.,1.)

end program simplemod </source> (from samples/procedures/simplemod/simplemod.f90)

Compiling & Running

When compiling the code a gravity.mod ﬁle is created
Machine-generated and readable “header” ﬁle containing detailed type, other information about contents of module
Not compatible between different compilers, versions.

<source lang="bash"> $ ls simplemod.f90

$ gfortran -o simplemod simplemod.f90 -Wall

$ ls gravity.mod simplemod simplemod.f90

$ ./simplemod

Gravitational constant =   6.6700000E-11
Force between 2 1kg masses at [1,0,0] and [0,0,1] is
 3.3350003E-11

</source>

Modules

function gravforce can “see” the modulewide parameter deﬁned above.
So can main program, through use statement.

<source lang="fortran"> <source lang="fortran"> module gravity

   implicit none
   real, parameter :: G  = 6.67e-11   ! MKS units

contains

   real function gravforce(x1,x2,m1,m2)
       implicit none
       real, dimension(3), intent(in) :: x1,x2
       real, intent(in) :: m1, m2
       real :: dist

       dist = sqrt(sum((x1-x2)**2))
       gravforce = G * m1 * m2 / dist**2
   end function gravforce

end module gravity

program simplemod

   use gravity
   implicit none

   print *, 'Gravitational constant = ', G
   print *, 'Force between 2 1kg masses at [1,0,0] &
             &and [0,0,1] is'

   print *, gravforce([1.,0.,0.],[0.,0.,1.],1.,1.)

end program simplemod </source> (from samples/procedures/simplemod/simplemod.f90)

use module, only :

Best practice is to only pull in from the module what you need
Otherwise, everything.
Adds some clarity and documentation, good for maintainability
(Note syntax for continuation of a string...)

<source lang="fortran"> module gravity

   implicit none
   real, parameter :: G  = 6.67e-11   ! MKS units

contains

   real function gravforce(x1,x2,m1,m2)
       implicit none
       real, dimension(3), intent(in) :: x1,x2
       real, intent(in) :: m1, m2
       real :: dist

       dist = sqrt(sum((x1-x2)**2))
       gravforce = G * m1 * m2 / dist**2
   end function gravforce

end module gravity

program simplemod2

   use gravity, only : G, gravforce
   implicit none

   print *, 'Gravitational constant = ', G
   print *, 'Force between 2 1kg masses at [1,0,0] &
             &and [0,0,1] is'
   
   print *, gravforce([1.,0.,0.],[0.,0.,1.],1.,1.)

end program simplemod2 </source> samples/procedures/simplemod/simplemod2.f90

Modules usually get their own ﬁles

For encapsulation
For ease of re-use
Here’s a slightly expanded module;
Let’s see how to compile it.
(Main program hasn’t changed much).

<source lang="fortran"> module gravity

   implicit none
   private

   character (len=8), parameter, public :: massunit="kilogram"
   character (len=8), parameter, public :: forceunit="Newton"
   public :: gravforce

   real, parameter :: G  = 6.67e-11   ! MKS units

contains

   real function distance(x1,x2)
       implicit none
       real, dimension(3), intent(in) :: x1, x2

       distance = sqrt(sum((x1-x2)**2))
   end function distance

   real function gravforce(x1,x2,m1,m2)
       implicit none
       real, dimension(3), intent(in) :: x1,x2
       real, intent(in) :: m1, m2
       real :: dist

       dist = distance(x1,x2)
       gravforce = G * m1 * m2 / dist**2
   end function gravforce

end module gravity </source> (from samples/procedures/multiﬁlemod/gravity.f90 )

Modules usually get their own ﬁles

Compiling gravity.f90 now gives both an .o ﬁle (containing the code) and the .mod ﬁle as before.
Compiling the main program (multiﬁlemod.f90) requires the .mod ﬁle.

<source lang="make"> FC=gfortran FFLAGS=-O3 -Wall

multifilemod: multifilemod.o gravity.o $(FC) -o $@ multifilemod.o gravity.o

%.mod: %.f90 $(FC) $(FFLAGS) -c $<

multifilemod.o: multifilemod.f90 gravity.mod $(FC) $(FFLAGS) -c $<

clean: rm -f *.o *~ *.mod multifilemod </source> (from samples/procedures/multiﬁlemod/Makeﬁle)

.mod needed for compilation

...because needs the type information of the constants,
and type information, number and type of parameters, for the function call.
Can’t compile without these

<source lang="fortran"> program simplemod2

   use gravity, only : gravforce, massunit, forceunit
   implicit none

   print *, 'Force between 2 1 ', massunit ,' masses ', &
            ' at [1,0,0] and [0,0,1] is'
   
   print *, gravforce([1.,0.,0.],[0.,0.,1.],1.,1.), forceunit

end program simplemod2 </source> (from samples/procedures/multiﬁlemod/multiﬁlemod.f90)

.o needed for linking

Linking, however, doesn’t require the .mod ﬁle
Only requires the .o ﬁle from the module code.
.mod ﬁle analogous (but better than) .h ﬁles for C code.

<source lang="make"> FC=gfortran FFLAGS=-O3 -Wall

multifilemod: multifilemod.o gravity.o $(FC) -o $@ multifilemod.o gravity.o

%.mod: %.f90 $(FC) $(FFLAGS) -c $<

multifilemod.o: multifilemod.f90 gravity.mod $(FC) $(FFLAGS) -c $<

clean: rm -f *.o *~ *.mod multifilemod </source> (from samples/procedures/multiﬁlemod/Makeﬁle)

Compiling and running

So compile ﬁles with modules ﬁrst, so those that need them have the .mod ﬁles
Link the .o ﬁles

<source lang="bash"> $ make gfortran -O3 -Wall -c gravity.f90 gfortran -O3 -Wall -c multifilemod.f90 gfortran -o multifilemod multifilemod.o gravity.o reposado-$ ./multifilemod

Force between 2 1 kilogram masses  at [1,0,0] and [0,0,1] is
 3.33500033E-11 Newton

</source>

Private and public

Not all of a module’s content need be public
Can give individual items public or private attribute
“private” makes everything private by default
Allows hiding implementation speciﬁc routines

<source lang="fortran"> module gravity

   implicit none
   private

   character (len=8), parameter, public :: massunit="kilogram"
   character (len=8), parameter, public :: forceunit="Newton"
   public :: gravforce

   real, parameter :: G  = 6.67e-11   ! MKS units

contains

   real function distance(x1,x2)
       implicit none
       real, dimension(3), intent(in) :: x1, x2

       distance = sqrt(sum((x1-x2)**2))
   end function distance

   real function gravforce(x1,x2,m1,m2)
       implicit none
       real, dimension(3), intent(in) :: x1,x2
       real, intent(in) :: m1, m2
       real :: dist

       dist = distance(x1,x2)
       gravforce = G * m1 * m2 / dist**2
   end function gravforce

end module gravity </source> ( from samples/procedures/multiﬁlemod/gravity.f90 )

Procedures

We’ve already seen procedures deﬁned in new style; let’s look more closely.
Biggest change: intent attribute to “dummy variables” (eg, parameters passed in/out).
Again, make expectations more explicit, compiler can catch errors, optimize.
Intent(in) - read only. Error to change.
Intent(out) - write only. Value undeﬁned before set.
Intent(inout) - read/write. (eg, modify region of an array)
Also documentation of a sort.

<source lang="fortran"> module procedures

contains

function square(x) result(xsquared)

     implicit none
     real :: xsquared
     real, intent(IN) :: x

     xsquared = x*x

end function square

function cube(x)

     implicit none
     real :: cube
     real, intent(IN) :: x

     cube = x*x*x

end function cube

subroutine squareAndCube(x, squarex, cubex)

     implicit none
     real, intent(in) :: x
     real, intent(out) :: squarex
     real, intent(out) :: cubex

     squarex = square(x)
     cubex   = cube(x)

end subroutine squareAndCube

end module procedures </source> ( from samples/procedures/funcsub/procedures.f90 )

Functions

Can be typed a couple of ways.
Old-style still works (real function square..)
Give a result variable different from function name; set that, type that result (xsquared)
Explicitly type the function name, set that as return value (cube)
Function return values don’t take intent - always out

<source lang="fortran"> function square(x) result(xsquared)

     implicit none
     real :: xsquared
     real, intent(IN) :: x

     xsquared = x*x

end function square

function cube(x)

     implicit none
     real :: cube
     real, intent(IN) :: x

     cube = x*x*x

end function cube

subroutine squareAndCube(x, squarex, cubex)

     implicit none
     real, intent(in) :: x
     real, intent(out) :: squarex
     real, intent(out) :: cubex

     squarex = square(x)
     cubex   = cube(x)

end subroutine squareAndCube </source> ( from samples/procedures/funcsub/procedures.f90 )

Procedure interfaces

The interface to a procedure consists of
- A procedure’s name
- The arguments, their names, types and all attributes
- For functions, the return value name and type
Eg, the procedure, with all the real code stripped out.
Like a C prototype, but more detailed info
.mod ﬁles contain explicit interfaces to all public module procedures.

<source lang="fortran"> function square(x) result(xsquared)

     implicit none
     real :: xsquared
     real, intent(IN) :: x

     xsquared = x*x

end function square

function cube(x)

     implicit none
     real :: cube
     real, intent(IN) :: x

     cube = x*x*x

end function cube

subroutine squareAndCube(x, squarex, cubex)

     implicit none
     real, intent(in) :: x
     real, intent(out) :: squarex
     real, intent(out) :: cubex

     squarex = square(x)
     cubex   = cube(x)

end subroutine squareAndCube </source> ( from samples/procedures/funcsub/procedures.f90 )

Procedure interfaces

To see where interfaces become necessary, consider this sketch of a routine to do trapezoid-rule integration
We want to integrate a passed-in function f, but we don’t know anything about it - type, # of arguments, etc.
Need to “type” f the same way you do with xlo, xhi, n.
You do that for procedures with interfaces

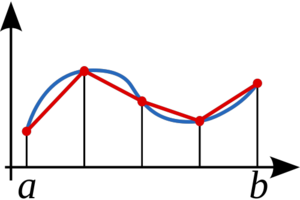
<source lang="fortran"> function integratefx(xlo, xhi, f, n)

integrate with trapezoid rule

....

   integer :: i
   real :: dx, xleft, xright

   integratefx = 0.
   dx = (xhi-xlo)/n
   xleft = xlo
   do i=0, n-1
       xright = xleft + dx
       integratefx = integratefx + dx*(f(xright)+f(xleft))/2.
       xleft = xright
   enddo

end function integratefx </source> (from samples/procedures/interface/integrate.f90 )

(from http://en.wikipedia.org/wiki/File:Trapezoidal_rule_illustration_small.svg )

Procedure interfaces

Deﬁne f as a parameter, give its type via an interface.
Can then use it, and at compile time compiler ensures function passed in matches thisinterface.

<source lang="fortran"> function integratefx(xlo, xhi, f, n)

integrate with trapezoid rule

   implicit none
   real, intent(in) :: xlo, xhi
   interface
       function f(x)
           implicit none
           real :: f
           real, intent(in) :: x        
       end function f
   end interface
   integer, intent(in) :: n
   real :: integratefx

   integer :: i
   real :: dx, xleft, xright

   integratefx = 0.
   dx = (xhi-xlo)/n
   xleft = xlo
   do i=0, n-1
       xright = xleft + dx
       integratefx = integratefx + dx*(f(xright)+f(xleft))/2.
       xleft = xright
   enddo

end function integratefx

</source> (from samples/procedures/interface/integrate.f90 )

Recursive procedures

By default, Fortran procedures cannot call themselves (recursion)
Can be enabled by giving the procedure the recursive attribute
Subroutines, functions
Recursive functions must use “result” keyword to return value.

<source lang="fortran"> recursive function integratefx(xlo, xhi, f, tol) result(integral)

integrate with trapezoid rule, simpsons rule;

if difference between two is larger than

relevant tolerance, subdivide region.

...variable declarations as before...

   dx = xhi-xlo
   xmid = (xlo+xhi)/2.
   trapezoid = dx*(f(xlo)+f(xhi))/2.
   simpsons = dx/6.*(f(xlo)+4.*f(xmid)+f(xhi))
   error = abs(trapezoid-simpsons)/(0.5*(trapezoid+simpsons))

   if (error > tol) then

too coarse; subdivide

       integral = integratefx(xlo,xmid,f,tol) + &
                  integratefx(xmid,xhi,f,tol) 
   else
       integral = trapezoid
   endif

end function integratefx </source> ( from samples/procedures/recursive/integrate.f90)

Pure procedures

Procedures are pure or impure depending on whether or not they have “side effects”:
- Changing things other than their dummy arguments
Modifying save variables
Modifying module data
Printing, etc.
Optimizations can be made for pure routines which can’t for impure
Label known-pure routines with the pure attribute.
Almost all the procedures we’ve seen so far are pure.

   pure subroutine axpy(a, x, y)

y = y + a*x

       implicit none
       real, intent(IN) :: a, x
       real, intent(INOUT) :: y

       y = y + a*x 
   end subroutine axpy

   subroutine printaxpy(a, x, y)

y = y + a*x

       implicit none
       real, intent(IN) :: a, x
       real, intent(INOUT) :: y

       print *, a, '*', x, ' + ', y, &
                ' = ', a*x+y
       y = a*x + y
   end subroutine printaxpy

</source> (from samples/procedures/purity/purity.f90)

Optional Arguments

Can make arguments optional by using the optional attribute.
Use present to test.
Often useful to clarify calling of procedure if many parameters have sensible defaults.
Avoid code duplication, wrappers of having one version of routine with default values, one with user-supplied
Can’t use tol if not present; have to use another variable.

<source lang="fortran"> recursive function integratefx(xlo, xhi, f, tol) result(integral)

....

   real, intent(in), optional :: tol

....

   real :: errtol

use parameter if passed,

else use default

   if (present(tol)) then
       errtol = tol
   else
       errtol = 1.e-6
   endif

....

   if (error > errtol) then

too coarse; subdivide

       integral = integratefx(xlo,xmid,f,errtol) + &
                  integratefx(xmid,xhi,f,errtol) 
   else
       integral = trapezoid
   endif

end function integratefx

</source> (from samples/procedures/optional/integrate.f90)

Optional Arguments

When calling the procedure, can use the optional argument or not.
Makes sense to leave optional arguments at end - easier to ﬁgure out what’s what when it’s omitted.

   print *, 'Integrating using default tol'
   approx = integratefx(0., 2*pi, sinesquared)
   print *, 'Approximate integral = ', approx
   print *, 'Exact integral = ', exact

   print *, 
   print *, 'Integrating using coarser tol'
   approx = integratefx(0., 2*pi, sinesquared, 0.01)
   print *, 'Approximate integral = ', approx

....

</source> (from samples/procedures/optional/optional.f90)

Keyword Arguments

To avoid ambiguity with omitted arguments - or really whenever you want - you can specify which value is which explicitly.
Don’t have to be in order.
Can clarify calls of routines with many arguments

....

   print *, 'Integrating using still coarser tol'
   approx = integratefx(xhi=2*pi, xlo=0., tol=0.5, &
                        f=sinesquared)
   print *, 'Approximate integral = ', approx

</source> (from samples/procedures/optional/optional.f90)

Procedures and Modules Summary

Modules let you bundle procedures, constants in useful packages.
Can have public, private components
Compiling them generates a .mod ﬁle (needed for compiling anything that does a “use modulename”) and an .o ﬁle (where the code goes, needed to link together the program).
New syntax for functions/subroutines: intent (IN/OUT/INOUT)
New syntax for function return values; result or explicit typing of function in argument list.
Procedures have interfaces, which are needed for (eg) passing functions
Optional/keyword arguments
Pure/recursive procedures

Hands On 2

In workedexamples/modules, have have pulled the PBM stuff out into a module.
Do the same with the hydro routines. What needs to be private? Public?
The common block (thankfully) only contains constants, can make those module parameters
~30 min

Fortran arrays

Fortran made for dealing with scientiﬁc data
Arrays built into language
The type information associated with an array includes rank (# of dimension), size, element type, stride..
Enables powerful optimizations, programmer-friendly features.
Can be manipulated like simple scalar variables
Elementwise addition, multiplication..

<source lang="fortran"> program basicarrays

   implicit none
   integer, dimension(5) :: a, b, c
   integer :: i

   a = [1,2,3,4,5]
   b = [(2*i+1, i=1,5)]

   print *, 'a = ', a
   print *, 'b = ', b

   c = a+b
   print *, 'c = ', c

   c = a*b + 1
   print *, 'a*b+1=', c

end program basicarrays </source> (from samples/arrays/basic.f90 )

Array constructors

Can have array constants like numerical constants
use [] or (/ /), then comma-separated list of values.
Implied do loops can be used in constructors
(Implied do-loop variables have to be deﬁned)

      x = [1,2,3,4,5]
      x = (/1,2,3,4,5/)
      x = [ (i,i=1,5)]
      a = [ ((i*j,j=1,3),i=1,5)]

</source>

Elementwise operations

Elementwise operations can be */+-, or application of an elemental function.
Math intrinsics are all elemental - applied to array, applies to every element.
Order of execution undeﬁned - allows vectorization, parallelization.

<source lang="fortran"> program elementwise

   implicit none
   real, dimension(10) :: x,y,z
   integer :: i
   real, parameter:: pi = 4.*atan(1.)

   x = [(2*pi*(i-1)/9.,i=1,10)]
   
   y = sin(x)
   z = x*x

   print *, x
   print *, y
   print *, z

end program elementwise </source> (from samples/arrays/elementwise.f90 )

Elemental Functions

User can create their own elemental functions
Label any scalar function with “elemental” should (until recently, must) be pure, so can be applied everywhere at same time.
Can be faster than loop.
Can also take multiple arguments: eg z = addsquare(x,y)

<source lang="fortran"> program elementalfn

   implicit none
   real, dimension(10) :: x,y,z
   integer :: i
   real, parameter:: pi = 4.*atan(1.)

   x = [(2*pi*(i-1)/9.,i=1,10)]
   
   y = sinesquared(x)
   z = sin(x)*sin(x)

   print *, x
   print *, y
   print *, z
   print *,z(::3)

contains

   elemental function sinesquared(x)
   implicit none
   real :: sinesquared
   real, intent(in) :: x

   sinesquared = sin(x)**2
   end function sinesquared

end program elementalfn </source> (from samples/arrays/elemental.f90 )

Array comparisons

Array comparisons return an array of logicals of the same size of the arrays.
Can use any and all to see if any or all of those logicals are true.

<source lang="fortran"> program comparearrays

   implicit none
   integer, dimension(5) :: a, b
   integer :: i

   a = [1,2,3,4,5]
   b = [(2*i-3, i=1,5)]

   print *, 'A = ', a
   print *, 'B = ', b

   if (any(a > b)) then
       print *, 'An A is larger than a B'
   endif            
   if (all(a > b)) then
       print *, 'All As ares larger than Bs'
   else if (all(b > a)) then
       print *, 'All Bs are larger than As'
   else 
       print *, 'A, B values overlap'
   endif

end program comparearrays </source> (from samples/arrays/compare.f90)

Array masks

These logical arrays can be used to mask several operations
Only do sums, mins, etc where the mask is true
Eg, only pick out positive values.
Many array intrinsics have this mask option

<source lang="fortran"> program mask

   implicit none
   integer, dimension(10) :: a
   logical, dimension(10) :: pos
   integer :: i

   a = [(2*i-7, i=1,10)]
   pos = (a > 0)

   print '(A,10(I4,1X))','A = ', a
   print *,'# of positive values:   ', count(pos)
   print *,'Sum of positive values: ', sum(a,pos)
   print *,'Minimum positive value: ', minval(a,pos)

end program mask </source> ( from samples/arrays/mask.f90 ) <source lang="bash"> $ ./mask A = -5 -3 -1 1 3 5 7 9 11 13

# of positive values:              7
Sum of positive values:           49
Minimum positive value:            1

</source>

Where construct

The where construct can be used to easily manipulate sections of array based on arbitrary comparisons.
Where construct => for whatever indices the comparison is true, set values as follow; otherwise, set other values.

<source lang="fortran"> program wherearray

   implicit none
   real, dimension(6) :: a, diva
   integer :: i

   a = [(2*i-6, i=1,6)]
   where (a /= 0)
       diva = 1/a
   elsewhere
       diva = -999
   endwhere

   print *,'a = '
   print '(6(F8.3,1X))',a
   print *,'1/a = '
   print '(6(F8.3,1X))',diva

end program wherearray </source> (from samples/arrays/where.f90) <source lang="bash"> $ ./where

a = 
 -4.000   -2.000    0.000    2.000    4.000    6.000
1/a = 
 -0.250   -0.500 -999.000    0.500    0.250    0.167

</source>

Forall construct

Forall is an array assignment statement
Each line in forall has to be independent. All done “at once” - no guarantees as to order
If (say) 2 lines in the forall, all of the ﬁrst line is done, then all of the second.
Any functions called must be pure
Can be vectorized or parallelized by compiler

<source lang="fortran"> program forallarray

   implicit none
   integer, dimension(6,6) :: a
   integer :: i,j

   a = -999
   forall (i=1:6, j=1:6, i/=j)
       a(i,j) = i-j
   endforall

   do i=1,6
       print '(6(I5,1X))',(a(i,j),j=1,6)
   enddo

end program forallarray </source> (from samples/arrays/forall.f90) <source lang="bash"> $ ./forall

-999    -1    -2    -3    -4    -5
   1  -999    -1    -2    -3    -4
   2     1  -999    -1    -2    -3
   3     2     1  -999    -1    -2
   4     3     2     1  -999    -1
   5     4     3     2     1  -999

</source>

Array Sections

Generalization of array indexing
Familiar to users of Matlab, IDL, Python..
Can use “slices” of an array using “index triplet”
[start]:[end][:step]
Default start=1, default end=size, default step=1.
Can be used for each index of multid array

a([start]:[end][:step])

a = [1,2,3,4,5,6,7,8,9,10]

a(7:) == [7,8,9,10] a(:3) == [1,2,3] a(2:4) == [2,3,4] a(::3) == [1,4,7,10] a(2:4:2) == [2,4] a(2) == 2 a(:) == [1,2,3,4,5,6,7,8,9,10] </source>

Array Sections

This sort of thing is very handy in numerical computation
Replace do-loops with clearer, shorter, possibly vectorized array operations
Bigger advantage for multidimensional arrays

<source lang="fortran"> program derivative

   implicit none
   real, dimension(10) :: x
   real, dimension(9) :: derivx
   integer :: i
   real, parameter:: pi = 4.*atan(1.), h=1.

   x = [(2*pi*(i-1)/9.,i=1,10)]
   
   derivx = ((x(2:10)-x(1:9))/h)
   print *, derivx

   do i=1,9
       derivx(i) = (x(i+1)-x(i))/h
   enddo
   print *, derivx

end program derivative </source> (from samples/arrays/derivative.f90)

Array Sections

The previous sorts of array sections - shifting things leftward and rightward - are so common there are intrinsics for them
positive shift shifts elements leftwards (or array bounds rightwards).
cshift does circular shift - shifting off the end of the array “wraps around”.
eoshift fills with zeros, or optional ﬁlling.
Can work on given dimension

a = [1,2,3,4,5]

cshift(a,1) == [2,3,4,5,1] cshift(a,-1) == [5,1,2,3,4] eoshift(a,1) ==[2,3,4,5,0] eoshift(a,-1)==[0,1,2,3,4] </source>

Other important array intrinsics

minval/maxval - ﬁnds min, max element in an array.
minloc/maxloc - ﬁnds location of min/max element
product/sum - returns product/sum of array elements
reshape - Adjusts shape of array data. Eg:

1,4

reshape([1,2,3,4,5,6],[3,2]) == 2,5

3,6

</source>

Linear algebra in Fortran

Comes built in with transpose, matmul, dot_product for dealing with arrays.
matmul also does matrix-vector multiplication
Either use these or system-provided BLAS libraries - never, ever write yourself.
Consider the following timings for a matrix multiplication - a naive triple loop, a clal to that matmul intrinsic, or an explicit call to a BLAS package.
factor of 100 difference!
Note that you can build gfortran to use fast (BLAS) routines for intrinsics...

Matrix Multiplication Times

...

   print *, 'Experiment with matrix size ', n
   print *, 'Times in seconds.'

   allocate(a(n,n))
   allocate(b(n,n))
   allocate(c(n,n))
   call random_number(a)
   call random_number(b)

   call tick(starttime)
   do j=1,n
       do i=1,n
           c(i,j) = 0.
           do k=1,n
               c(i,j) = c(i,j)+a(i,k)*b(k,j)
           enddo
       enddo
   enddo
   looptime = tock(starttime)

   call tick(starttime)
   c = matmul(a,b)
   matmultime = tock(starttime)

   call tick(starttime)
   call sgemm('N','N',n,n,n,1.,a,n,b,n,0.,c,n)
   sgemmtime = tock(starttime)

   print *, 'Triple-loop time:      ', looptime
   print *, 'matmul intrinsic time: ', matmultime
   print *, 'SGEMM lapack call time:', sgemmtime

...

</source>

<source lang="bash"> $ ./matmul 2500 Experiment with matrix size

Triple-loop time:

   149.63400

matmul intrinsic time:

   10.370000

SGEMM lapack call time:

   1.4809999

</source> (gfortran 4.6, compiled -O3 -march=native using Intel MKL 10.3 for sgemm) (program from samples/arrays/matmul.f90)

Linear algebra in Fortran

Things like transposes work, too:
see samples/arrays/matrix.f90

<source lang="fortran"> program matvec

   implicit none
   integer, dimension(4,5) :: a
   integer, dimension(5,4) :: at
   integer, dimension(4,4) :: aat
   integer :: i

   a = reshape([(i,i=1,4*5)],[4,5])
   at = transpose(a)
   print *,'A = '
   call printmat(a)
   print *,'A^T = '
   call printmat(at)

   aat = matmul(a,at)
   print *,'A . A^T = '
   call printmat(aat)

...

</source>

<source lang="bash"> $ ./matrix

A = 
  1    5    9   13   17
  2    6   10   14   18
  3    7   11   15   19
  4    8   12   16   20
A^T = 
  1    2    3    4
  5    6    7    8
  9   10   11   12
 13   14   15   16
 17   18   19   20
A . A^T = 
565  610  655  700
610  660  710  760
655  710  765  820
700  760  820  880
A . A^T subarray = 
610  660  710
655  710  765
700  760  820

</source>

Array sizes and Assumed Shape

Printmat routine here is interesting - don’t pass (a,rows,cols), just a.
Can assume a rank-2 array, and get size at runtime.
Simpliﬁes call, and eliminates possible inconsistency: what if rows, cols is wrong?
size(array,dim) gets the size of array in the dim dimension.
Assumed shape arrays (eg, dimension(:,:)) much better than older ways of passing arrays:

integer nx, ny

integer a(nx,ny)

or worse,

integer a(*,ny)

Information is thrown away, possibility of inconsistency.
Here, (:,:) means we know the rank, but don’t know the size yet.

   subroutine printmat(a)
   implicit none
   integer, dimension(:,:) :: a
   integer :: nr, nc, i, j

   nr = size(a,1)
   nc = size(a,2)
   do i=1,nr
       print '(99(I4,1X))', (a(i,j), j=1,nc)
   enddo
   end subroutine printmat

</source> (from samples/arrays/matrix.f90)

Allocatable Arrays

So far, all our programs have had ﬁxed-size arrays, set at compile time.
To change problem size, have to edit code, recompile.
Has some advantages (optimization, determinism) but very inﬂexible.
Would like to be able to request memory at run time, make array of desired size.
Allocatable arrays are arguably most important addition to Fortran.

Allocate(), Deallocate()

Give array a deferred size (eg, dimension(:)) and the attribute allocatable.
When time to allocate it, use allocate(a(n)).
Deallocate with deallocate(a).
In between, arrays can be used as any other array.
If allocation fails (not enough memory available for request), program will exit.
Can control this by checking for an optional error code, allocate(a(n),stat=ierr)
Can then test if ierr>0 (failure condition) and handle gracefully.
In scientiﬁc programming, the default behaviour is often ﬁne, if abrupt - you either have enough memory to run the problem, or you don’t.

<source lang="fortran"> program allocarray

   implicit none
   integer :: i, n
   integer, dimension(:), allocatable :: a

   n = 10
   allocate(a(n))
   a = [(i, i=2,20,2)]

   print *,'A = '
   print *,a

   deallocate(a)

end program allocarray </source> (from samples/arrays/allocatable.f90 )

get_command_argument()

Previous version still depended on a compiled-in number.
Can read from ﬁle or from console, but Fortran now has standard way to get command-line arguments
Get the count of arguments, and if there’s at least one argument there, get it, read it as integer, and allocate array.

<source lang="fortran"> program allocarray2

   implicit none
   integer :: i, n
   integer, dimension(:), allocatable :: a
   character(len=30) :: arg

   if (command_argument_count() < 1) then
       print *,'Use: allocatable N, '//&
               ' where N is array size.'
       stop
   endif

   call get_command_argument(1, arg)
   read( arg,'(I30)'), n
    
   print *,'Allocating array of size ', n
   allocate(a(n))

   a = [(i,i=1,n)]
   print *, a
   
   deallocate(a)

end program allocarray2 </source> (from samples/arrays/allocatable2.f90) <source lang="bash"> $ ./allocatable2

Use: allocatable N,  where N is array size.

$ ./allocatable2 3

Allocating array of size	     3

1 2 3

$ ./allocatable2 5

Allocating array of size	     5

1 2 3 4 5 </source>

Hands on #3

Use array functionality to simplify hydro code -- don't need to pass, array size, and can simplify mathematics using array operations.
In workedexamples/arrays, have modiﬁed hydro to allocate u, and pbm to just take array.
Do the same with the ﬂuid dynamic routines in solver.f90
~30 min

Fortran Pointers

Pointers, or references, refer to another variable.
Eg, p does not contain a real value, but a reference to another real variable.
Once associated with another variable, can read/write to it as if it were stored “in” p.

<source lang="fortran"> real, target :: x = 3.2 real, pointer:: p p => x

p

x 3.2 </source> samples/pointers/ptr1.f90

Fortran Pointers

Pointers are either associated, null, or undeﬁned; start out life undeﬁned.
Can associate them to a variable with => , or mark them as not associated with any valid variable by pointing it to null().
Reading value from or writing value to a null pointer will cause errors, probably crash.
Fortran pointers can’t point just anywhere.
Must reference a variable with the same type, that has the target attribute.

<source lang="fortran"> real, target :: x = 3.2 real, pointer:: p p => null() p

x </source>

Fortran Pointers

Pointers can reference other pointers.
Actually references what they’re pointing to.

<source lang="fortran"> real, target :: x = 3.2 real, pointer:: p1, p2 p1 => x p2 => p1 p1 p2

x 3.2 </source>

Allocating a pointer

Pointer doesn’t necessarily have to have another variable to target
Can allocate memory for p to point to that does not belong to any other pointer.
Must deallocate it when done

<source lang="fortran"> real, pointer:: p allocate(p) p = 7.9 p 7.9

</source> samples/pointers/ptr2.f90

What are they good for? (1)

Pointers are essential for creating, maintaining dynamic data structures
Linked lists, trees, heaps..
Some of these can be sort-of implemented in arrays, but very awkward
Adaptive meshes, treebased particle solvers need these structures.

http://en.wikipedia.org/wiki/File:Singly-linked-list.svg http://en.wikipedia.org/wiki/File:Max-Heap.svg

What are they good for? (2)

A pointer can be of array type, not just scalar
Fortran pointers + fortran arrays are quite interesting; can create “views” of subarrays

<source lang="fortran"> real, target, dimension(7) :: x real, pointer:: p(:) p => x(2:6)

p x 1

2

3

4

5

6

7 </source> samples/pointers/views.f90

Hands on #4

Use pointers to provide views into subsets of the arrays in solver.f90 to clarify the functions.
In workedexamples/pointers, have started the process with cﬂ, hydroﬂux; try tackling tvd1d, others.
~30 min

Derived Types and Objects

Often, groups of variables naturally go together to represent a larger structure
Whenever you ﬁnd yourself passing the same group of variables to several routines, a good candidate for a derived type.

<source lang="fortran"> type griddomain

   real :: xmin, xmax
   real :: ymin, ymax
   real :: nx, ny
   real, dimension(:,:) :: u

endtype griddomain

type(griddomain) :: g g % xmin = -1 g % xmax = +1 </source>

Derived Types and Objects

Consider interval arithmetic (good for quantiﬁcation of uncertainties, etc).
An interval inherently has two values associated with it - the end points.
Can make this a type.
Note can access the ﬁelds in the type with “%”
typename (ﬁeld1val,ﬁeld2val..) initializes a value of that type.
Can pass values of this type to functions, etc., just like a built-in type.

(from samples/derivedtypes/simple/intervalmath.f90 )

Procedures using types

Can start creating library of routines that operate on these new interval types.
Procedures can take the new type as arguments, functions can return the new type.

(from samples/derivedtypes/intervalfunctions/intervalmath.f90 )

Procedures using types

Would prefer not to have to treat integer and real intervals so differently in main program
Different types, but adding should be similar.
Would like to be able to call “addintervals” and have language call the right subroutine, do the right thing.
Similar to how intrinsics work - sin() works on any kind of real, matmult() works on integer, real, or complex matricies.

samples/derivedtypes/genericintervals/interval2.f90

Generic Interfaces

Generic Interfaces
addintintervals and addrealintervals share the same interface, (two input parameters, one function return), but different types.
Put them behind the same interface.
Now, a call to addintervals is resolved at compile time to one or the other.

samples/derivedtypes/genericintervals/intervalmath.f90

Generic Interfaces

Note that everything is private except what is explicitly made public.
Types are public.
Generic interfaces are public.
Type speciﬁc routines are not.
Program using interval math sees only the generic interfaces.

samples/derivedtypes/genericintervals/intervalmath.f90

Generic interfaces

Call to addintervals or subtract intervals goes to the correct typespeciﬁc routine.
As does print interval.
Could create routines to add real to int interval, etc and add to the same interface.

samples/derivedtypes/genericintervals/interval2.f90

Operator overloading

An inﬁx operator is really just “syntactic sugar” for a function which takes two operands and returns a third.

<source lang="fortran" a = b (op) c => function op(b,c) returns a

a=b => subroutine assign(a,b) </source>

Operator overloading

Here, we’ve deﬁned two subroutines which set intervals based on an array - 2 ints for an integer interval, or 2 reals for a real interval

samples/derivedtypes/intervaloperators/intervalmath.f90

Generic interfaces

Once this is done, can use assignment operator,
Or add, subtract multiply intervals.
Can even compose them in complex expressions! Functions automatically composed.

samples/derivedtypes/intervaloperators/interval3.f90

Type bound procedures

Types can have not only variables, but procedures.
Takes us from a type to what is usually called a class.

(from samples/derivedtypes/intervaltypebound/intervalmath.f90 )

Type bound procedures

Called like one accesses a ﬁeld - %
Operates on data of the particular variable it is invoked from

samples/derivedtypes/intervaltypebound/interval3.f90

Type bound procedures

It is implicitly passed as it’s ﬁrst parameter the variable itself.
Can take other arguments as well.

samples/derivedtypes/intervaltypebound/intervalmath.f90

Object oriented programming

F2003 onwards can do full object oriented programing.
Types can be derived from other types, inheriting their ﬁelds and type-bound procedures, and extending them.
Goes beyond scope of today, but this is the starting-off point.

Interoperability with other languages

Large scientiﬁc software now frequently uses multiple languages, either within a single code or between codes.
Right tool for the job!
Need to know how to make software interact.
Here we’ll look at C/Fortran code calling each other, and calling Fortran code from python.

C-interoperability

iso_c_binding module contains deﬁnitions for interacting with C
Types, ways to bind procedures to C, etc.
Allows you to call C routines, or bind Fortran routines in a way that they can be called by C.

Calling a C routine from Fortran

As with the case of calling a passed-in function, need an explicit prototype.
Tells compiler what to do with “sqrtc” function when called.

samples/C-interop/call-c-fn/main.f90

Calling a C routine from Fortran

BIND(C) - tells compiler/ linker will have a C-style, rather than fortran-style name in object ﬁle.
Can optionally supply another name; otherwise, will default to procedure name.
Here we’re calling it sqrtc to avoid Fortran sqrt() function.
The value the function takes and returns are C doubles; that is, reals of kind(c_double).
Also deﬁned: c_ﬂoat, integers of kind c_int, c_long, etc.

Calling a C routine from Fortran

C function arguments by default are passed by value; Fortran by default are passed by reference.
Passed by value - values copied into function
Passed by reference pointers to values copied in.
value attribute for C-style arguments.
Compiling - just make sure to link in C library you’re calling
And that’s it.

<source lang="bash"> $ make gfortran -c main.f90 gfortran -o main main.o -lm

$ ./main x = 2.0000000000000000 C sqrt(x) = 1.4142135623730951 Fortran sqrt(x) = 1.4142135623730951 </source>

C strings

When using C strings, you have to remember that C terminates strings with a special character
C_NULL_CHAR
Dealing with functions that return strings is hairier, as they return a pointer, not an array.

<source lang="bash"> $ make gfortran-mp-4.4 -c main.f90 gfortran-mp-4.4 -o main main.o -lc $ ./main 1234 = 1234 </source> (from samples/C-interop/c-strings/main.f90 )

Calling Fortran from C

To write Fortran routines callable from C, bind the subroutine to a C name
Can optionally give it a different name, as above
And make sure arguments are of C types.

samples/C-interop/c-call-fortran/froutine.f90

Calling Fortran from C

Here, we’ll do something a little trickier and pass C dynamic arrays
In Fortran, we accept the arguments as C pointers
We then associate them with fortran pointers to arrays of shape [nx] (1d arrays here)
Then we can do the usual Fortran array operations with them.
The single scalar argument passed back we just treat as an intent(out) variable
Of type c_ﬂoat.

(from samples/C-interop/c-call-fortran/froutine.f90 )

More advanced

Handling arbitrary C code is possible
Passing C structs -- create a Fortran derived type with the same ﬁelds, use BIND(C) in deﬁning the type.
C “multidimensional arrays” - have to be careful, they may not be contiguous! Follow pointers.
Even taking passed function pointers to C

functions is possible

(from samples/C-interop/functionptr )

Fortran calling C, which calls Fortran

samples/C-interop/valueref/driver.f90

samples/C-interop/valueref/croutine.c

samples/C-interop/valueref/froutine.f90

$ ./main

<source lang="bash"> $ ./main (1) In the FORTRAN routine before call to C (1) i = 15 x = 2.0000000000000000 (2) In the C routine, got i=15, *x=2.000000 (2) Changed x (3) In the FORTRAN routine called by C (3) Got product p = 30.000000000000000 (1) In the FORTRAN routine after call to C (1) i = 15 x = 3.0000000000000000 prod = 30.000000000000000 </source>

samples/C-interop/valueref/Makeﬁle

F2py

Comes with scipy, a widely-installed (by scientists) python package.
Wraps fortran in python, allows you to easily interface.
fwrap is another option

http://www.scipy.org/F2py

* Will only use solver module.

Unfortunately, f2py isn’t quite smart enough to understand using parameters to size arrays, so global replace ‘nvars’=4
module load use.experimental gcc python/2.7.1 intel/12
“f2py -m hydro_solver -h hydro_solver.pyf solver.f90”

* generates the following header ﬁle (hydro_solver.pyf)

Comment out stuff we don’t need (lower-level routines)
f2py -c --fcompiler=gfortran hydro_solver.pyf solver.f90

$ ipython

<source lang="bash"> In [1]: import hydro_solver In [2]: hydro_solver.solver. hydro_solver.solver.cﬂ hydro_solver.solver.gamma hydro_solver.solver.hydroﬂux hydro_solver.solver.idens hydro_solver.solver.iener hydro_solver.solver.imomx

hydro_solver.solver.imomy hydro_solver.solver.initialconditions hydro_solver.solver.timestep hydro_solver.solver.tvd1d hydro_solver.solver.xsweep hydro_solver.solver.xytranspose

In [2]: hydro_solver.solver.idens Out[2]: array(1, dtype=int32) In [3]: import numpy In [4]: u = hydro_solver.solver.initialconditions(100,100) In [5]: import pylab In [6]: pylab.imshow(u[1,:,:]) In [7]: for i in range(100) ...dt = hydro_solver.solver.timestep(u) In [8]: pylab.imshow(u[1,:,:]) </source>

Coarrays

In F2008, objects can also have a “codimension”.
An object with a codimension can be “seen” across processes
Right now, only intel v 12 supports this

samples/coarrays/simple.f90

Coarrays

1

A B

2

A B

N

...

A B

num_images independant processes

Coarrays

1

A B

2

A B

N

...

A B

num_images independant processes

A[1] B[N]

Independent, parallel tasks can “see” each other’s data as easily as an array index.

Sychronization

When accessing other processor’s data, must ensure that tasks are synchronized
Don’t want to read task 1’s data before read is complete!
sync all

samples/coarrays/broadcast.f90

Sychronization

Other synchronization tools:
sync images([..]) syncs only images in the list provided
critical - only one image can enter block at a time
lock - ﬁner-grained control than critical.
atomic operations.

samples/coarrays/broadcast.f90

1d Diffusion Eqn

Calculate heat diffusion along a bar
Finite difference; calculate second derivative using neighbours
Get new temperature from old temperatures

1 -2 1

1d Diffusion Eqn

Initial conditions:
Use pointers to point to new, old temperatures
1..totpoints+2 (pts 1, totpoints+1 “ghost cells)
Setup x, orig temperature, expected values

samples/coarrays/diffusion/diffusion.f90

1d Diffusion Eqn

Evolution:
Apply BCs
Apply ﬁnite difference stencil to all real data points

samples/coarrays/diffusion/diffusion.f90

1d Diffusion Eqn

Output calculated values and theory to ﬁle output.txt
Note: Fortran2008, can use “newunit” to ﬁnd, use an unused IO unit

samples/coarrays/diffusion/diffusion.f90

$ ./diffusion

[..] $ gnuplot [..] gnuplot> plot 'output.txt' using 1:2 with points title 'Simulated', 'output.txt' using 1:3 with lines title 'Theory'

Coarray Diffusion

Now we’ll try this in parallel
Each image runs it’s part of the problem (totpoints/num_images())
Communications is like boundary condition handling - except boundary data must be obtained from neighbouring image.

Coarray Diffusion

Everything’s the same except we are only responsible for locpoints points, starting at start.
Once calculated, we never need totpoints again. All arrays are of size (locpoints), etc.
For simplicity, we assume here everything divides evenly.

samples/coarrays/diffusion/diffusion-coarray.f90

Coarray Diffusion

Boundary exchange; if we have interior neighbours, get updated data from them so we can calculate our new data
Note: can’t use pointers here, coarrays can’t be targets.
Sync all around boundary exchange a little heavy handed; could just sync neighbours.

samples/coarrays/diffusion/diffusion-coarray.f90

Coarray Diffusion

<source lang="fortran"> temperature()[leftneigh]

temperature() temperature()[rightneigh]

1 2 3 ...

lnpts+2 </source>

Coarray Diffusion

Everything else exactly the same.
For I/O, we each output our own ﬁle, preﬁxed by our image number
(eg, 1-output.txt, 2output.txt...)

samples/coarrays/diffusion/diffusion-coarray.f90

$ export FOR_COARRAY_NUM_IMAGES=3

3 images

$ ./diffusion-coarray [..] $ gnuplot [..] gnuplot> plot '1-ics.txt' using 1:2, '2-ics.txt' using 1:2, '3-ics.txt' using 1:2 </source>

gnuplot> plot '1-output.txt' using 1:2, '2-output.txt' using 1:2, '3output.txt' using 1:2, '1-output.txt' using 1:3 with lines title 'Theory',

'2-output.txt' using 1:3 with lines title 'Theory', '3-output.txt' using 1:3 with lines title 'Theory'

Parallel Matrix Multiplication

Consider matrix operations, where matrix is decomposed onto images in blocks
A given image has corresponding blocks in A, B, responsible for that block in C.

A

B X C =

Parallel Matrix Multiplication

Block matrix multiply exactly like matrix multiply, except each operation is a submatrix operation
matmul instead of “*”.
For simplicity, we’ll assume square decomposition.

A

B X C =

Parallel Matrix Multiplication

Each image gets its own block of a, b, c.
Note [nrows,*]. Coarrays can have any corank(eg, number of codimensions)
Here, we make decomposition nrows x ncols.
Can set decomposition array-by-array.

samples/coarrays/blockmatrix.f90

Parallel Matrix Multiplication

Allocation, deallocation of coarrays is like a sync all
Forces synchronization across all images
Any particular coarray must have same size, co-size across all images

samples/coarrays/blockmatrix.f90

Parallel Matrix Multiplication

This is the entire parallel multiplication operation.
a[myrow,k] gets the entire a block from image at myrow,k.
matmul works with those blocks, updates c with new term.

samples/coarrays/blockmatrix.f90

Coarray Summary

Coarrays are powerful, simple-to-use addition to parallel programming models available
Will be widely available soon
Basic model implemented in Cray fortran for ~10 yrs; well tested and understood.
Typically implemented with MPI under the hood; can give performance similar to MPI with fewer lines of code.
Other languages have similar extensions (UPC based on C, Titanium based on Java) but are not part of languages’ standard.

Closing Hints

Always give the compiler info it needs to help you by being as explicit as possible
implicit none, end [construct] [name], parameters for constants, intent in/out, use only, etc.
Always get as much info from compiler as possible - always use -Wall (gfortran) or -warn all (ifort).

Useful Resources

http://fortranwiki.org/
- Reference source; has all standards; Fortran2003/2008 status of major compilers
http://en.wikipedia.org/wiki/Fortran_language_features
- Succinct summary of new features (spotty past F95)
http://stackoverﬂow.com/questions/tagged/fortran
- ( Programmers Questions & Answers